Triangular Sums
I was recently working on a fun programming puzzle, and wasn’t quite sure what to call the thing I was doing. It was like a factorial, but it wasn’t quite that (working with sums, rather than products). The code looked like this:
function not_a_factorial(num) {
if (num === 0) return 0;
return num + not_a_factorial(num - 1);
}
A few minutes of curious Googling later, and I have a better method name: this is called a Triangular Sum, and the concept is demonstrated by the graphic below:
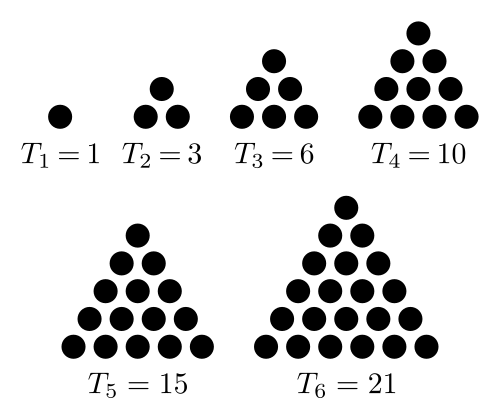
If you consider the input number as the base of the triangle, and add each row together, you get the end result. A triangle, if you will!
✨ Perf Bonus!
Like many recursive algorithms, this one can be improved with some basic memoization:
const TRIANGULARS = [0]
function triangular(num) {
if (!isNaN(TRIANGULARS[num])) return TRIANGULARS[num];
if (num === 0) return 0;
return TRIANGULARS[num] = num + triangular(num - 1);
}
The idea is that since the triangular sum of each number builds on the triangular sum of the preceding one, we can actually build an array of triangular sums using the num itself as the index. This takes advantage of the fact that JavaScript doesn’t throw IndexOutOfBounds exceptions, but rather just returns undefined (which isNaN).